Turunan adalah pengukuran terhadap bagaimana fungsi
berubah seiring perubahan nilai input, atau secara umum turunan menunjukkan
bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam
menemukan turunan disebut diferensiasi.
TURUNAN PERTAMA
Misalnya
y merupakan fungsi dari x atau dapat ditulis juga y=f(x). Turunan dari y
terhadap x dinotasikan sebagai berikut:
Dengan
menngunakan definisi turunan diatas dapat diturunkan beberapa rumus-rumus
turunan, yaitu 1. Jika
diketahui
Perhatikan
contoh berikut :
2. Jika
diketahui y=C dan
Perhatikan
contoh berikut :
3. Untuk
y=f(x)+g(x) maka
Perhatikan
contoh berikut :
atau dapat juga
kita misalkan f(x)=u dan g(x)=v sehingga rumus turunan u.v=u’v+uv’
contoh :
5.
6. Untuk
turunan lain tersaji dalam penjelasan dibawah ini.
TURUNAN KEDUA
Turunan kedua
dari y=f(x) terhadap x dinotasikan sebagai berikut
Turunan kedua
merupakan turunan yang diperoleh dengan menurunkan kembali turunan pertama.
Perhatikan contoh berikut :
a. Menentukan
gradien garis singgung kurva
Jika diketahui
garis g menyinggung kurva y=f(x) pada titik (a,f(a)) sehingga gradien untuk g
adalah
Penyelesaian :
Sehingga
gradien garis singgung kurva y=x²+3x dititik (1,-4) adalah m=y(1)=2.1+3=5
b. Menentukan
apakah interval tersebut naik atau turun
kurva y =f(x)
naik jika f ‘ (x) >0 dan kurva y=f(x) turun jika f ‘ (x) <0.
Lalu bagaimana cara menentukan f ‘ (x) > 0 atau f ‘ (x)
<0 ? kita gunakan garis bilangan dari f ‘ (x). Perhatikan contoh berikut :
Tentukanlah
interval naik dan interval turun dari fungsi y=x³+3x²-24x !
Jawab :
y=f(x)=x³+3x²-24x
→f ‘ (x)=3x²+6x-24=3(x²+2x-8)=3(x+4)(x-2)
Berdasarkan
garis bilangan yang diperoleh diatas :
f ‘ (x) >0
untuk x<-4 dan x>2 yang merupakan interval untuk fungsi naik.
F ‘ (x) <0
untuk -4 < x < 2 yang merupakan interval untuk fungsi turun.
c. Menentukan
nilai maksimum dan nilai minimum
Nilai maksimum
dan nilai minimum fungsi ini sering disebut juga dengan nilai ekstrim atau
nilai stasioner fungsi, yang dapat diperoleh pada f ‘ (x)=0 untuk fungsi
y=f(x). Untuk lebih jelasnya perhatikan contoh berikut.
Tentukan nilai
ekstrim dari fungsi y=x³-3x²-24x-7 !
Jawab :
y’=3x²-6x-24
nilai ekstrim
diperoleh dari y’=o maka
3x²-6x-24 = 0
(x²-2x-8)=0
(x-4)(x+2)=0
x1=4 ; x2=-2
Berdasarkan
garis bilangan diatas :
Fungsi maksimum
pada x=-2 sehingga nilai balik maksimumnya yaitu :
f(-2)=(-2)³-3(-2)²-24(-2)-7
f(-2)=21
Fungsi minimum
pada x=4 sehingga nilai balik minimumnya yaitu :
f(4)=(4)³-3(4)²-24(4)-7
f(4)=-87





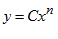

















Tidak ada komentar:
Posting Komentar